poldigital2011 - Mapas de Karnaugh 5 variables

MAPAS DE KARNAUGH DE 5 VARIABLES

Recordemos que para conseguir el mapa de 5 variables, debe proyectarse el mapa de 4 variables. El abatimiento es hacia la derecha ya que el número de variables es impar. La figura adjunta muestra la proyección del mapa de 4 variables.

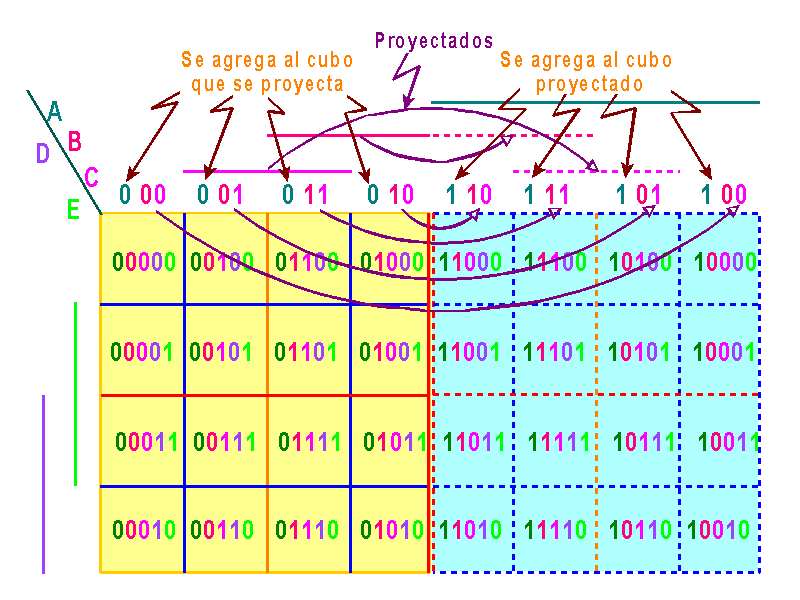
Obsérvese que al mapa que se proyecta se le antepone un 0 y al proyectado un 1. También, se ha asociado a cada celda el número binario correspondiente, el cual se obtuvo asignando el valor binario a cada variable en dicha celda.

Sustituyendo el número binario de cada celda por su equivalente decimal, se obtiene el mapa de Karnaugh para 5 variables que se empleará para minimizar funciones de conmutación de 5 variables independientes. La figura adjunta presenta este mapa.

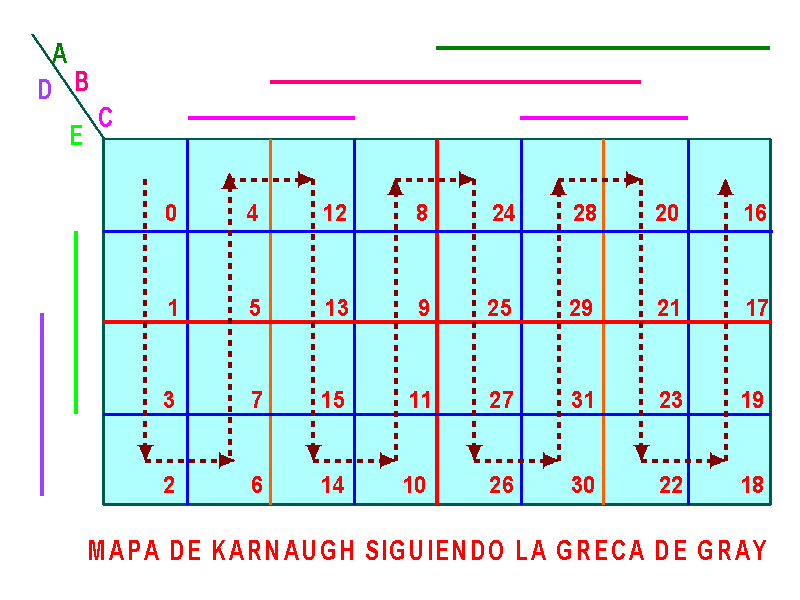
Para generar el código de Gray para 5 variables, se traza la greca de Gray sobre el mapa K para 5 variables y se escribe el código binario asociado a cada celda.

La figura adjunta muestra la greca de Gray sobre el mapa de Karnaugh de 5 variables.

A continuación se presentan algunos ejemplos que muestran la aplicación del mapa para la minimización de funciones de conmutación de 5 variables binarias.

EJEMPLO 6. Minimice las siguientes funciones, empleando el método de Karnaugh:

F1 = Sumaminitérminos (0,1,3,8,9,11,16-17,19,24,25,29-31)

F2 = Sumaminitérminos (0-4,6,9,10,15-20,22,23,25,26,31)

SOLUCION

Las siguientes figuras presentan los mapas K para F1 y F2:

Las funciones reducidas son:

F1(A,B,C,D,E) = C'D' + B'C'D + ABCD + A'BDE + ABD'E
(1) (2) (3) (4) (5)

F2(A,B,C,D,E) = B'C' + B'E' + C'D'E + C'DE' + AB'D + BCDE
(1) (2) (3) (4) (5) (6)

EJEMPLO 7. Hay 5 personas que actúan como jueces en un competencia dada. El voto de cada uno de ellos se indica con un 1 (pasa) o 0 (fracasa) en un línea de señal. Las 5 líneas de señal son las entradas a un circuito lógico combinacional. Las reglas de la competencia permiten sólo la disensión de un voto. Si la votación es 2-3 o 3-2, la competencia debe continuar. El circuito lógico debe tener dos salidas, XY. Si el voto es 4-1 o 5-0 para pasar, XY=11. Si el voto es 4-1 o 5-0 para fracasar, XY=00; si el voto es 3-2 o 2-3 para continuar, XY=10.

Diseñe un circuito mínimo de suma de productos.

SOLUCION

La siguiente tabla agrupa las condiciones del enunciado:

REGLA	OPCIÓN				X	Y
	1		0
PARA PASAR PARA FRACASAR PARA CONTINUAR	5 0 3	4 1 2	0 5 2	1 4 3	1 0 1	1 0 0

En base a la tabla anterior, se construye la siguiente:

TABLA FUNCIONAL
DEC	A	B	C	D	E	X	Y	DEC	A	B	C	D	E	X	Y
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0	0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1	0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1	0 0 0 1 0 1 1 1 0 1 1 1 1 1 1 1	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1	16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31	1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1	0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1	0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 1

De la tabla funcional, se obtienen las siguientes funciones de conmutación canónicas:

X(A,B,C,D,E) = Sumaminitérminos (3,5-7,9-15,17-31)

Y(A,B,C,D,E) = Sumaminitérminos (15,23,27,19-31)

Reduciendo por mapas de Karnaugh: Para mayor claridad, se presenta a X(A, B, C, D, E) en dos mapas:

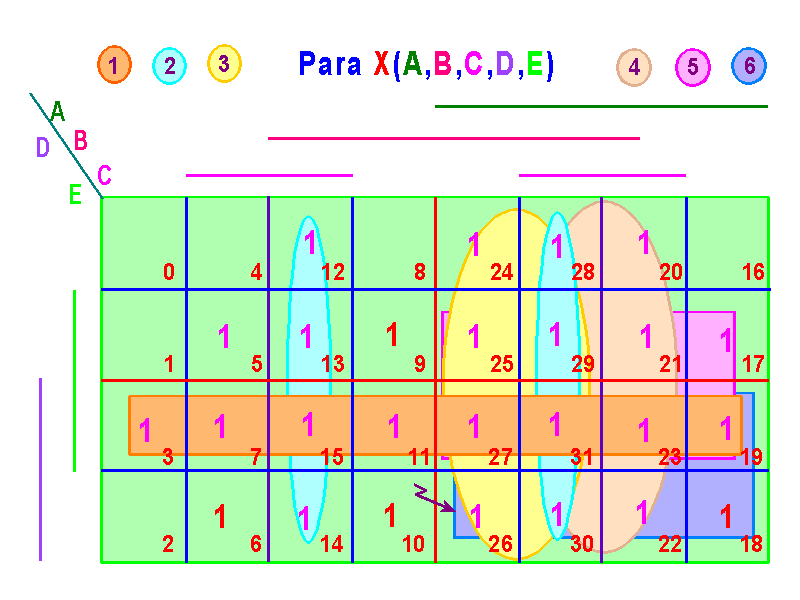
El mapa para Y(A, B, C, D, E) es:

Para ver el gráfico seleccione la opción "Descargar" del menú superior

De los mapas anteriores se tienen las siguientes funciones reducidas:

X(A,B,C,D,E) = DE + BC + AB + AC + AE + AD + CE + CD + BE + BD
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)

Y(A,B,C,D,E) = ABCE + ABCD + ACDE + BCDE + ABDE
(1) (2) (3) (4) (5)

El logigrama se presenta en la siguiente figura:

Para ver el gráfico seleccione la opción "Descargar" del menú superior

2.5 MAPAS DE KARNAUGH DE 6 VARIABLES

Siguiendo el mismo criterio para la obtención de los mapas anteriores, proyectando el mapa inmediatamente anterior, se obtiene el mapa K para 6 variables:

Para ver el gráfico seleccione la opción "Descargar" del menú superior

EJEMPLO 8. Minimizar las siguientes funciones por el método de Karnaugh:

a) Z = Sumaminitérminos (7,14,28,56) + Sumaindiferentes (0-6,8-13,16-27,29,32-55,57-59,61)

b) Z = Prodmaxitérminos (15,30,31,60, 62,63) Prodindiferentes (0-6,8-13,16-27,29,32-55,57-59,61)

SOLUCION

Obsérvese que las funciones, en ambos incisos, son las mismas, una expresada como minitérminos y la otra como maxitérminos. Las siguientes figuras muestran los mapas para los incisos a) y b), respectivamente:

Para ver el gráfico seleccione la opción "Descargar" del menú superior

De los mapas anteriores, se obtienen las siguientes funciones reducidas:

Z(A,B,C,D,E,F) = C' + D' + A'E' + B'F'
(1) (2) (3) (4)

Z(A,B,C,D,E,F) = (C' + F') (B' + E')(A' + B' + D')
(1) (2) (3)

2.6 EJERCICIOS

1. Minimice las siguientes funciones booleanas, utilizando el método de Karnaugh:

a) f(A,B,C,D) = Sumaminitérminos (0,4,6,10,11,13)

b) f(w,x,y,z) = Prodmaxitérminos (3,4,5,7,11,12,14,15)

c) f(a,b,c,d) = Sumaminitérminos (3,5,7,11,15)

d) f(A,B,C,D,E) = Prodmaxitérminos (0,1,2,8,9,11,15-19,24,25,29-31)

e) f(A,B,C,D,E,F) = Sumaminitérminos (0,2,4,5,7,8,16,18,24,32,36,40,48,56)

2. Un número primo es aquel que sólo es divisible entre si mismo y la unidad. Diseñe un circuito lógico mínimo que detecte todos los números primos entre 0 y 31. La salida F(A, B, C, D, E), donde A es la variable de mayor peso binario, será igual a 1, si y sólo si los cinco bits de entrada representan un número primo. Realice el logigrama utilizando inversores y compuertas No Y.

3. En uno de los laboratorios de una compañía químico farmacéutica se elaboran 14 distintas soluciones a partir de las componentes W, X, Y y Z. Estas sustancias pesan 800, 400, 200 y 100 mg, respectivamente. Las soluciones depositadas en frascos se transportan por medio de una banda hasta una báscula. Si el peso indicado en la báscula es uno de los siguientes: 200, 500, 700, 800, 1100, 1400 o 1500 mg, entonces un dispositivo electromecánico F, después de agregar al compuesto la sustancia Q, sellará el frasco sobre la báscula y lo apartará de la banda; de otro modo, el frasco permanecerá abierto y la banda lo transportará hacia otra etapa del proceso. Además, por las condiciones previas del proceso, no es posible que lleguen a la báscula ni frascos vacíos, ni frascos que contengan las siguientes sustancias: WY, YZ, WX o WZ; todas las demás combinaciones sí pueden llegar hasta la báscula.

Determinar la función booleana del circuito combinatorio L que acciona el dispositivo F y minimizar haciendo uso de condiciones irrelevantes. Realizar el circuito mediante inversores y compuertas No O.

4. En la torre de control de un patio de ferrocarril,un controlador debe seleccionar la ruta de los furgones de carga que entran a una sección del patio, mismos que provienen del punto A, como puede verse en el tablero de control de la figura adjunta. Dependiendo de las posiciones de los conmutadores, un furgón puede llegar a uno cualesquiera de los cuatro destinos. Otros furgones pueden llegar desde los puntos B o C.

Diseñe un circuito, con inversores y compuertas No O, que reciba como entradas las señales S1 a S5, indicadores de las posiciones de los conmutadores correspondientes, y que encienda una lámpara D0 a D3, indicando el destino al que llegará el furgón proveniente de A.

Para los casos en que los furgones puedan entrar de B o C (S2 o S3 en la posición 0), todas las lámparas de salida deben encenderse, indicando que un furgón proveniente de A, no puede llegar con seguridad a su destino.

NOTA: S1 bit de mayor peso binario.

5. Un circuito lógico tiene 5 entradas A, B, C, D y E (donde A es la de mayor peso binario). Cuatro de las entradas representan un dígito decimal en BCD (Decimal Codificado en Binario, por sus siglas en inglés). La primera entrada, A, es de control.

Cuando el control está en 0 lógico, la salida Z e igual a 0 si el número decimal es impar y 1 si es par.

Cuando el control está en 1 lógico, la salida Z es igual a 1 cuando la entrada en múltiplo de 3, en caso contrario es 0.

Considerando las condiciones irrelevantes, diseñe un circuito mínimo utilizando sólo inversores y compuertas No O.

NOTA: Considere al 0 como un número par.

6. Un técnico de un laboratorio químico tiene 4 productos A, B, C y D. Cada producto debe encontrarse en uno cualesquiera de dos recipientes de almacenamiento.

Periódicamente, se requiere cambiar uno o más productos de un recipiente a otro. La naturaleza de los productos es tal, que es peligroso guardar A y B juntos a menos que D esté presente en el mismo recipiente. También es peligroso almacenar B y C juntos a menos que D esté presente.

Este proceso no permite que alguno de los tanques esté vacío.

Obtener el circuito mínimo de la expresión de una variable Z que deberá tener el valor de 0 para cada situación peligrosa de almacenamiento, utilizando sólo inversores y compuertas No O.

NOTA: Considere a A como la variable de mayor peso binario.

7. Un posicionador de eje, proporciona una señal de 4 bits que indica la posición de un eje en pasos de 30°. Utilizando el código de Gray, el cual se muestra en la siguiente tabla, diseñe un circuito (realización mínima de suma de productos) que produzca una salida que indique en dónde se encuentra el eje.

POSICIÓN DEL EJE	SALIDA DEL DECODIFICADOR		POSICIÓN DEL EJE	SALIDA DEL DECODIFICADOR
0°<= P <=30° 30°< P <=60° 60°< P <=90° 90°< P <=120° 120°< P <=150° 150°< P <=180°	0 0 11 0 0 1 0 0 1 1 0 0 1 1 1 0 1 0 1 0 1 0 0		180°< P <=210° 210°< P <=240° 240°< P <= 270° 270°< P <=300° 300°< P <=330° 330°< P <=360°	1 1 0 0 1 1 0 1 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 1

Obtenga el logigrama utilizando inversores y compuertas No Y.

8. Obtener el diagrama lógico mínimo, con inversores y compuertas No O, de un circuito de 5 entradas: Dos de datos A y B y tres de control C2, C1 y C0.

La función de salida depende de los ocho posibles estados de las señales de control, de acuerdo a la siguiente tabla:

CONTROL (DECIMAL)	F
0	1
1	A + B
2	(A B)'
3	A OEX B
4	(A OEX B)'
5	A B
6	(A + B)'
7	0

Considere a C2 y A como las variables de mayor peso binario, respectivamente.

9. El sistema nervioso humano, incluyendo el cerebro, está hecho de células especializadas llamadas neuronas. Cada neurona tiene sinapsis (puntos de interconexión, como se muestra en la figura adjunta) de excitación y sinapsis de inhibición. Una neurona produce una salida 1 si el número de sinapsis de excitación con pulsos 1 excede el número de sinapsis de inhibición con pulsos 1 por al menos el valor de umbral de la neurona.

Determine la función booleana f(a,b,c,d,e) de emisión de pulsos a través del canal de salida (axón) en el modelo de la figura, bajo las siguientes condiciones:

(C1) Valor del umbral = 1 [es decir, se produce una salida 1 si el número de sinapsis de excitación con pulsos 1, excede por al menos uno el número de sinapsis de inhibición con pulsos 1], y

(C2) Siempre que haya al menos un pulso 1 en alguna sinapsis del puerto de excitación, habrá al menos un pulso 1 en alguna sinapsis del puerto de inhibición [es decir, no es posible -en este modelo restringido- que existan pulsos 1 en el puerto de excitación si no existe al menos un pulso 1 en el puerto de inhibición].

Minimizar f(a, b, c, d, e) haciendo uso de las condiciones irrelevante (C2). Realizar el logigrama utilizando inversores y compuertas No Y.

10. Textura es la organización de una superficie como un conjunto de elementos repetidos. En un proceso automático para clasificar texturas artificiales, un sensor de 4 puntos (figura adjunta) envía señales a un circuito combinatorio cuya tarea es discriminar (emitiendo pulsos 1) los siguientes elementos:

En todos los casos que inspecciona el sensor se activan al menos 2 puntos de la rejilla (es decir, no se presentan casos en los cuales se activa tan solo un punto ni casos en los que no se activa ningún elemento)

Minimizar la función booleana f(a,b,c,d,e) a la salida del circuito discriminador, haciendo uso de las condiciones irrelevantes. Realizar el circuito mediante inversores y compuertas No O.

11. En una fábrica un dispositivo con 5 fotoceldas (figura adjunta), registra los caracteres formados abriendo pequeñas ranuras en una tarjeta de control. Si en la tarjeta registrada hay uno de los símbolos:

(Para el símbolo I son válidas las dos posiciones), entonces el dispositivo acciona un taladro.

En el proceso no hay tarjetas con alguno de los caracteres adjuntos:

(Todos los caracteres restantes si son válidos)

¿Cuál es la función booleana a la salida del dispositivo que acciona el taladro? Minimizar la función y realizar el logigrama utilizando sólo inversores y compuertas No Y.

12. Se desea diseñar e instrumentar un circuito combinatorio mínimo de dos entradas con dos bits cada una, sobre las cuales se codifican dos de los cuatro tipos de sangra existentes y a su salida se obtenga una señal que informe sobre la posibilidad o imposibilidad de la transfusión de uno de ellos sobre el otro, dadas las siguientes reglas de compatibilidad entre ellos.

Los tipos de sangre son 4: A, B, AB y O.

El tipo O puede donar a cualquier otro tipo, pero sólo puede recibir de él mismo.

El tipo AB puede recibir de cualquier otro tipo pero sólo puede donar a AB.

La clase A puede donar a A o a AB y recibir de A u O únicamente.

Por último, el tipo B puede donar al mismo B o al tipo AB y recibir de B u O.

La señal de salida deberá ser 1 cuando la transfusión propuesta en las entradas sea permitida.

Realizar el logigrama utilizando inversores y compuertas No O.

13. En un sistema de detección luminosa que tiene el arreglo mostrado en la figura adjunta, se genera una señal de salida con valor de 1 únicamente cuando dos fotoceldas adyacentes están activadas, siempre y cuando la fotocelda del centro esté también activada.

NOTA: No es posible, en este sistema, que exista una señal de salida 0 o 1 si no hay al menos tres fotoceldas activadas.

Considerando a A como la variable más significativa, obtener el logigrama mínimo, considerando las condiciones indiferentes y utilizando sólo inversores y compuertas No Y.

14. Un robot de juguete -llamado U-2- está diseñado para ser capaz de seguir una trayectoria (previamente programada por medio de controles que el robot tiene en la espalda) avanzando cuadro por cuadro en una área de 5x6 cuadros. El robot U-2 puede realizar una de las cuatro acciones siguientes:

(D) Girar (sobre su eje vertical) 90° a la derecha y luego avanzar al centro del siguiente cuadro si su pequeño cerebro recibe la señal binaria 01.

(I) Girar 90° a la izquierda y luego avanzar al centro del siguiente cuadro si su diminuto cerebro percibe la señal binaria 10.

(F) Avanzar al frente un cuadro si su cerebro recibe la señal 00.

(A) Hacer alto si su cerebro recibe la señal 11.

Programar el robot para que recorra el laberinto de la Figura (a). Determinar las funciones booleanas del par de estímulos binarios que recibe el minicerebro del robot durante este recorrido y minimizarlas mediante mapas de Karnaugh. (En este problema hay condiciones irrelevantes -parte de la solución consiste en encontrarlas).

Los controles en la espalda del U-2 están localizados en dos áreas: En el área I se indicará el cuadro inicial mediante los controles de dos posiciones a, b, c, d y e [como se muestra en la Figura (c)]; si el control a se presiona del lado derecho, el peso de la variable a se contabilizará para determinar el número asignado al cuadro inicial (lo mismo ocurrirá para el resto de las variables). En el área II se programa la trayectoria por medio de 30 controles de tres posiciones cada uno.